[LeetCode] 279. Perfect Squares

https://leetcode.com/problems/perfect-squares/

Perfect Squares - LeetCode

279. Perfect Squares

 

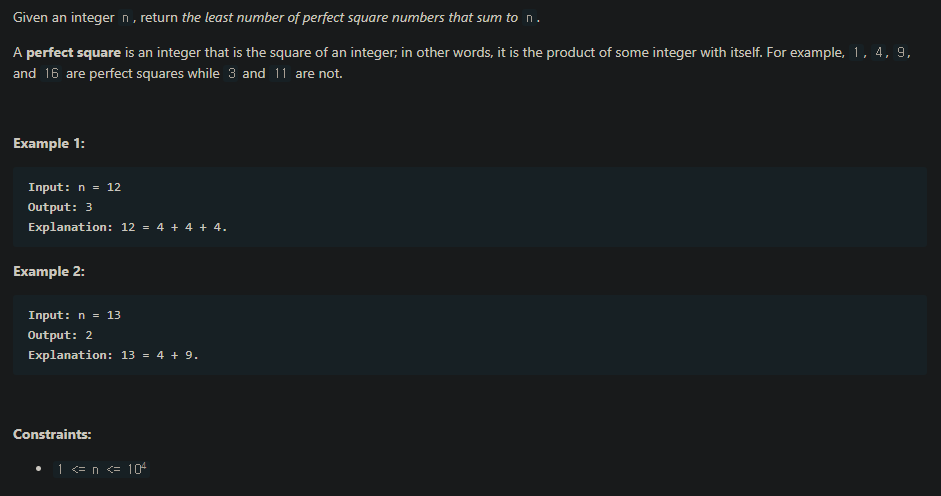
어떤 수 n이 주어진다.

이 n은 자연수의 제곱수들의 합으로만 이루어졌을때,

이 제곱수 개수의 최소값을 구하는 문제이다.

 

처음 시도했던 방법은

범위가 10000까지 이므로, 

ans 배열은 10000까지 만든후,

i = 1부터 10000까지, j = 1부터 i/2까지

ans[i] = min(ans[j] + ans[i-j]) 로 구하는 방법이다.

보통 1억개의 연산까지 시간초과로 안되는걸로 알고 있고,

이 경우에는 모든 연산을 10000번째를 기준으로 해도 10000*5000 = 50,000,000번의 연산이기에 가능했다.

class Solution {
public:
    int numSquares(int n) {
        int squares[10005];
        int ans[10005];
        for (int i=1; i<=10000; i++) squares[i] = 0;
        for (int i=1; i<=100; i++) squares[i*i] = 1;
        for (int i=1; i<=n; i++) {
            if (squares[i]) {
                ans[i] = 1;
                continue;
            }
            int m = INT_MAX;
            for (int j=1; j<=i/2; j++) m = ans[j] + ans[i-j]<m?ans[j]+ans[i-j]:m;
            ans[i] = m;
        }
        return ans[n];
    }
};

 

하지만 10000보다 크게 나오면 터질것을 알고 있기에 다른방법을 궁리해보았다.

앞의 방법과 비슷하긴 한데,

덧셈은 제곱수로만 이루어진다에 초점을 맞추었다.

 

가장먼저 ans를 1로만 더해졌을 때 수로 세팅한다.

즉 1=1, 2=1+1, 3=1+1+1,...개로, ans[i] = i 로 세팅한다.

그 후, 다음 제곱수는 4가 되는데,

4부터 4를 포함한 수로 계산을 하여 둘중 최소값으로 저장을 해준다.

즉 4 = 1+1+1+1 => 4로,

5 = 1+1+1+1+1 = 1+4로...

 

앞의 방법과 마찬가지로 4부터 해서 ans[i] = min(ans[i], ans[4] + ans[i-4]) 로 계산해주면 된다.

다음은 9차례로 9부터 시작해서 다시 계산해준다.

이렇게 i^2이 n보다 작을때까지 계산해주면 위의 방법보다는 시간을 단축하여 계산할 수 있다.

풀이는 아래와 같다.

 

class Solution {
public:
    int numSquares(int n) {
        int ans[10005];
        for (int i=1; i<=n; i++) ans[i] = i;
        for (int i=2; i*i<=n; i++) {
            ans[i*i] = 1;
            for (int j=i*i+1; j<=n; j++) ans[j] = min(ans[j], ans[i*i]+ans[j-i*i]);
        }
        return ans[n];
    }
};